Физические свойства жидкости

Что такое плотность жидкости

Плотность жидкости — это отношение массы жидкости к объёму, который она занимает.

Если две жидкости одинаковой массы налить в сосуды, то их объемы будут разниться. Причина этому — плотность, т.е. расстояние между молекулами и атомами, образующими внутреннее строение. Эта величина скалярная и обозначается буквой ρ. В литературе можно встретить и другие обозначения, например D и d (в переводе с латинского densitans).

Примечание

Понятие плотности касается однородных веществ, в т.ч. в жидком состоянии. Если однородность отсутствует, говорят о средней плотности либо плотности в одной точке.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Обычная вода при температуре 4С имеет максимальное ее значение — 1000 кг/м3. Многие жидкие продукты питания имеют близкое значение плотности. Например, обезжиренное молоко, раствор уксуса, вино. В то же время для сока из ананаса аналогичное значение составляет 1084, из винограда — 1361, апельсина — 1043 кг/м3. Пиво имеет плотность 1030 кг/м3.

Многие жидкости менее плотны, чем вода, это:

• спирт этиловый (789 кг/м3);
• нефть (от 730 до 940 кг/м3);
• бензин (от 680 до 800 кг/м3);
• ДТ (879 кг/м3).

Зависимость от температуры

Все измерения нужно проводить при стандартной комнатной температуре, потому что в горячем и холодном состоянии значения будут другими, не равными, а различными, Если возникла потребность в проведении нестандартных определений, нужно измерить температуру, затем плотность и по таблице получить показания, соответствующие нормальным условиям.

Плотность воды находится в заметной зависимости от температуры, например разница между значениями, измеренными при 18 и при 20 ℃, составляет 0,4 кг/м3.

При охлаждении плотность немного понижается, и при нагревании также происходит ее постепенное понижение. В этом вода отличается от всех других веществ, которые при охлаждении становятся плотнее.

Феномен объясняется способностью полярных водных молекул образовывать конгломераты, которые иногда называют ассоциатами или кластерами. В зависимости от величины этих образований, их пространственной формы, наличия воздушных полостей между группами масса стандартной единицы объема имеет разные значения.

В агрегатном состоянии пара все молекулы находятся на большом расстоянии друг от друга, притягиваться не могут, поэтому значения плотности маленькие. Уменьшение плотности при нагревании происходит постепенно, например при 60 ℃ показатель равен 983,2 кг/м3, а при 100 °С – 958,4 кг/м3.

При замерзании, еще до образования льда, кластеры приобретают форму, содержащую большое количество воздушных полостей, что объясняет также понижение значения плотности. Кстати, по этой причине лед плавает на поверхности северных морей и океанов. Если бы он имел большую плотность, айсберги постепенно оседали бы в виде ледяных пластов на дно, заполняя акваторию по всей глубине, не оставляя шансов на выживание морским рыбам и млекопитающим этих климатических зон.

Плотность воды в зависимости от температуры

Принято считать, что плотность воды равна 1000 кг/м3, 1000 г/л или 1 г/мл, но часто ли мы задумываемся при какой температуре получены эти данные?

Максимальная плотность воды достигается при температуре 3,8…4,2°С. В этих условиях точное значение плотности воды составляет 999,972 кг/м3. Такая температурная зависимость плотности характерна только для воды. Другие распространенные жидкости не имеют максимума плотности на этой кривой — их плотность равномерно снижается по мере роста температуры.

Вода существует как отдельная жидкость в диапазоне температуры от 0 до максимальной 374,12°С — это ее критическая температура, при которой исчезает граница раздела между жидкостью и водяным паром. Значения плотность воды при этих температурах можно узнать в таблице ниже. Данные о плотности воды представлены в размерности кг/м3 и г/мл.

В таблице приведены значения плотности воды в кг/м3 и в г/мл (г/см3), допускается интерполяция данных. Например, плотность воды при температуре 25°С можно определить, как среднее значение от величин ее плотности при 24 и 26°С. Таким образом, при температуре 25°С вода имеет плотность 997,1 кг/м3 или 0,9971 г/мл.

Значения в таблице относятся к пресной или дистиллированной воде. Если рассматривать, например, морскую или соленую воду, то ее плотность будет выше — плотность морской воды равна 1030 кг/м3. Плотность соленой воды и водных растворов солей можно узнать в этой таблице. Плотность воды при различных температурах — таблица

t, °С	ρ, кг/м3	ρ, г/мл	t, °С	ρ, кг/м3	ρ, г/мл	t, °С	ρ, кг/м3	ρ, г/мл
999,8	0,9998	62	982,1	0,9821	200	864,7	0,8647
0,1	999,8	0,9998	64	981,1	0,9811	210	852,8	0,8528
2	999,9	0,9999	66	980	0,98	220	840,3	0,8403
4	1000	1	68	978,9	0,9789	230	827,3	0,8273
6	999,9	0,9999	70	977,8	0,9778	240	813,6	0,8136
8	999,9	0,9999	72	976,6	0,9766	250	799,2	0,7992
10	999,7	0,9997	74	975,4	0,9754	260	783,9	0,7839
12	999,5	0,9995	76	974,2	0,9742	270	767,8	0,7678
14	999,2	0,9992	78	973	0,973	280	750,5	0,7505
16	999	0,999	80	971,8	0,9718	290	732,1	0,7321
18	998,6	0,9986	82	970,5	0,9705	300	712,2	0,7122
20	998,2	0,9982	84	969,3	0,9693	305	701,7	0,7017
22	997,8	0,9978	86	967,8	0,9678	310	690,6	0,6906
24	997,3	0,9973	88	966,6	0,9666	315	679,1	0,6791
26	996,8	0,9968	90	965,3	0,9653	320	666,9	0,6669
28	996,2	0,9962	92	963,9	0,9639	325	654,1	0,6541
30	995,7	0,9957	94	962,6	0,9626	330	640,5	0,6405
32	995	0,995	96	961,2	0,9612	335	625,9	0,6259
34	994,4	0,9944	98	959,8	0,9598	340	610,1	0,6101
36	993,7	0,9937	100	958,4	0,9584	345	593,2	0,5932
38	993	0,993	105	954,5	0,9545	350	574,5	0,5745
40	992,2	0,9922	110	950,7	0,9507	355	553,3	0,5533
42	991,4	0,9914	115	946,8	0,9468	360	528,3	0,5283
44	990,6	0,9906	120	942,9	0,9429	362	516,6	0,5166
46	989,8	0,9898	125	938,8	0,9388	364	503,5	0,5035
48	988,9	0,9889	130	934,6	0,9346	366	488,5	0,4885
50	988	0,988	140	925,8	0,9258	368	470,6	0,4706
52	987,1	0,9871	150	916,8	0,9168	370	448,4	0,4484
54	986,2	0,9862	160	907,3	0,9073	371	435,2	0,4352
56	985,2	0,9852	170	897,3	0,8973	372	418,1	0,4181
58	984,2	0,9842	180	886,9	0,8869	373	396,2	0,3962
60	983,2	0,9832	190	876	0,876	374,12	317,8	0,3178

Следует отметить, что при увеличении температуры воды (выше 4°С) ее плотность уменьшается. Например, по данным таблицы, плотность воды при температуре 20°С равна 998,2 кг/м3, а при ее нагревании до 90°С, величина плотности снижается до значения 965,3 кг/м3. Удельная масса воды при нормальных условиях значительно отличается от ее плотности при высоких температурах. Средняя плотность воды, находящейся при температуре 200…370°С намного меньше ее плотности в обычном температурном диапазоне от 0 до 100°С.

Смена агрегатного состояния воды приводит к существенному изменению ее плотности. Так, величина плотности льда при 0°С имеет значение 916…920 кг/м3, а плотность водяного пара составляет величину в сотые доли килограмма на кубический метр. Следует отметить, что значение плотности воды почти в 1000 раз больше плотности воздуха при нормальных условиях.

Кроме того, вы также можете ознакомиться с таблицей плотности веществ и материалов.

Физические свойства воды при температуре от 0 до 100°С

В таблице представлены следующие физические свойства воды: плотность воды ρ, удельная энтальпия h, удельная теплоемкость Cp, теплопроводность воды λ, температуропроводность воды а, вязкость динамическая μ, вязкость кинематическая ν, коэффициент объемного теплового расширения β, коэффициент поверхностного натяжения σ, число Прандтля Pr. Физические свойства воды приведены в таблице при нормальном атмосферном давлении в интервале от 0 до 100°С.

Физические свойства воды существенно зависят от ее температуры. Наиболее сильно эта зависимость выражена у таких свойств, как удельная энтальпия и динамическая вязкость. При нагревании значение энтальпии воды значительно увеличивается, а вязкость существенно снижается. Другие физические свойства воды, например, коэффициент поверхностного натяжения, число Прандтля и плотность уменьшаются при росте ее температуры. К примеру, плотность воды при нормальных условиях (20°С) имеет значение 998,2 кг/м3, а при температуре кипения снижается до 958,4 кг/м3.

Такое свойство воды, как теплопроводность (или правильнее — коэффициент теплопроводности) при нагревании имеет тенденцию к увеличению. Теплопроводность воды при температуре кипения 100°С достигает значения 0,683 Вт/(м·град). Температуропроводность H2O также увеличивается при росте ее температуры.

Следует отметить нелинейное поведение кривой зависимости удельной теплоемкости этой жидкости от температуры. Ее значение снижается в интервале от 0 до 40°С, затем происходит постепенный рост теплоемкости до величины 4220 Дж/(кг·град) при 100°С.

Физические свойства воды при атмосферном давлении — таблица

t, °С →	10	20	30	40	50	60	70	80	90	100
ρ, кг/м3	999,8	999,7	998,2	995,7	992,2	988	983,2	977,8	971,8	965,3	958,4
h, кДж/кг	42,04	83,91	125,7	167,5	209,3	251,1	293	335	377	419,1
Cp, Дж/(кг·град)	4217	4191	4183	4174	4174	4181	4182	4187	4195	4208	4220
λ, Вт/(м·град)	0,569	0,574	0,599	0,618	0,635	0,648	0,659	0,668	0,674	0,68	0,683
a·108, м2/с	13,2	13,7	14,3	14,9	15,3	15,7	16	16,3	16,6	16,8	16,9
μ·106, Па·с	1788	1306	1004	801,5	653,3	549,4	469,9	406,1	355,1	314,9	282,5
ν·106, м2/с	1,789	1,306	1,006	0,805	0,659	0,556	0,478	0,415	0,365	0,326	0,295
β·104, град-1	-0,63	0,7	1,82	3,21	3,87	4,49	5,11	5,7	6,32	6,95	7,52
σ·104, Н/м	756,4	741,6	726,9	712,2	696,5	676,9	662,2	643,5	625,9	607,2	588,6
Pr	13,5	9,52	7,02	5,42	4,31	3,54	2,93	2,55	2,21	1,95	1,75

Примечание: Температуропроводность в таблице дана в степени 108 , вязкость в степени 106 и т. д. для других свойств. Размерность физических свойств воды выражена в единицах СИ.

Плотность растворов

Плотность раствора — это сумма массовых (массовых) концентраций компонентов этого раствора.

Массовая (массовая) концентрация каждого заданного компонента ρ _i в растворе суммируется с плотностью раствора.

ρзнак равно∑яϱя{\ Displaystyle \ rho = \ сумма _ {я} \ varrho _ {я} \,}

Выраженный как функция плотностей чистых компонентов смеси и их объемного участия , он позволяет определять избыточные молярные объемы :

ρзнак равно∑яρяVяVзнак равно∑яρяφязнак равно∑яρяVя∑яVя+∑яVEя{\ displaystyle \ rho = \ sum _ {i} \ rho _ {i} {\ frac {V_ {i}} {V}} \, = \ sum _ {i} \ rho _ {i} \ varphi _ { i} = \ sum _ {i} \ rho _ {i} {\ frac {V_ {i}} {\ sum _ {i} V_ {i} + \ sum _ {i} {V ^ {E}} _ {я}}}}

при условии отсутствия взаимодействия между компонентами.

Зная соотношение между избыточными объемами и коэффициентами активности компонентов, можно определить коэффициенты активности.

VE¯язнак равнорТ∂пер⁡γя∂п{\ displaystyle {\ overline {V ^ {E}}} _ {i} = RT {\ frac {\ partial \ ln \ gamma _ {i}} {\ partial P}}}

Значения других единиц, равные введённым выше

 открыть 

 свернуть 

Метрическая система

плотность воды при 100°C → тонна на кубометр (т/м³)
плотность воды при 100°C → килограмм на кубометр (кг/м³)
плотность воды при 100°C → грамм на кубометр (г/м³)
плотность воды при 100°C → миллиграмм на кубометр (мг/м³)
плотность воды при 100°C → килограмм на литр (кг/л)
плотность воды при 100°C → грамм на литр (г/л)
плотность воды при 100°C → миллиграмм на литр (мг/л)
плотность воды при 100°C → килограмм на кубический дециметр (кг/дм³)

плотность воды при 100°C → грамм на кубический дециметр (г/дм³)
плотность воды при 100°C → миллиграмм на кубический дециметр (мг/дм³)
плотность воды при 100°C → килограмм на кубический сантиметр (кг/см³)
плотность воды при 100°C → грамм на кубический сантиметр (г/см³)
плотность воды при 100°C → миллиграмм на кубический сантиметр (мг/см³)
плотность воды при 100°C → килограмм на миллилитр (кг/мл)
плотность воды при 100°C → грамм на миллилитр (г/мл)
плотность воды при 100°C → миллиграмм на миллилитр (мг/мл)

Единицы:

тонна на кубометр
(т/м³)

 /
килограмм на кубометр
(кг/м³)

 /
грамм на кубометр
(г/м³)

 /
миллиграмм на кубометр
(мг/м³)

 /
килограмм на литр
(кг/л)

 /
грамм на литр
(г/л)

 /
миллиграмм на литр
(мг/л)

 /
килограмм на кубический дециметр
(кг/дм³)

 /
грамм на кубический дециметр
(г/дм³)

 /
миллиграмм на кубический дециметр
(мг/дм³)

 /
килограмм на кубический сантиметр
(кг/см³)

 /
грамм на кубический сантиметр
(г/см³)

 /
миллиграмм на кубический сантиметр
(мг/см³)

 /
килограмм на миллилитр
(кг/мл)

 /
грамм на миллилитр
(г/мл)

 /
миллиграмм на миллилитр
(мг/мл)

 открыть 

 свернуть 

Британские и американские единицы

плотность воды при 100°C → фунты на кубический ярд (lb/yd³)
плотность воды при 100°C → фунты на кубический фут (lb/ft³)
плотность воды при 100°C → фунты на кубический дюйм (lb/in³)
плотность воды при 100°C → фунты на галлон США (lb/gal)
плотность воды при 100°C → фунты на британский галлон
плотность воды при 100°C → фунты на бушель США

плотность воды при 100°C → унции на кубический ярд (oz/yd³)
плотность воды при 100°C → унции на кубический фунт (oz/ft³)
плотность воды при 100°C → унции на кубический дюйм (oz/in³)
плотность воды при 100°C → унции на галлон США (oz/gal)
плотность воды при 100°C → унции на британский галлон
плотность воды при 100°C → унции на бушель США

Единицы:

фунты на кубический ярд
(lb/yd³)

 /
фунты на кубический фут
(lb/ft³)

 /
фунты на кубический дюйм
(lb/in³)

 /
фунты на галлон США
(lb/gal)

 /
фунты на британский галлон

 /
фунты на бушель США

 /
унции на кубический ярд
(oz/yd³)

 /
унции на кубический фунт
(oz/ft³)

 /
унции на кубический дюйм
(oz/in³)

 /
унции на галлон США
(oz/gal)

 /
унции на британский галлон

 /
унции на бушель США

 открыть 

 свернуть 

Английские инжернерные и британские гравитационные единицы

плотность воды при 100°C → Слаг на кубический ярд (slug/yd³)

плотность воды при 100°C → Слаг на кубический фут (slug/ft³)
плотность воды при 100°C → Слаг на кубический дюйм (slug/in³)

Единицы:

Слаг на кубический ярд
(slug/yd³)

 /
Слаг на кубический фут
(slug/ft³)

 /
Слаг на кубический дюйм
(slug/in³)

 открыть 

 свернуть 

Естественнные единицы

В физике естественные единицы измерения базируются только на фундаментальных физических константах. Определение этих единиц никак не связано ни с какими историческими человеческими построениями, только с фундаментальными законами природы.

плотность воды при 100°C → планковская плотность (L⁻³M)

Единицы:

планковская плотность
(L⁻³M)

 открыть 

 свернуть 

Плотности различных веществ

Это лишь несколько примеров. Все плотности даны для стандартных условий температур и давления.

плотность воды при 100°C → плотность воздуха на уровне моря
плотность воды при 100°C → плотность воды при 0°C
плотность воды при 100°C → плотность воды при 4°C
плотность воды при 100°C → плотность воды при 100°C
плотность воды при 100°C → плотность льда
плотность воды при 100°C → плотность алмаза

плотность воды при 100°C → плотность железа
плотность воды при 100°C → плотность меди
плотность воды при 100°C → плотность серебра
плотность воды при 100°C → плотность свинца
плотность воды при 100°C → плотность золота
плотность воды при 100°C → плотность платины

Единицы:

плотность воздуха на уровне моря

 /
плотность воды при 0°C

 /
плотность воды при 4°C

 /
плотность воды при 100°C

 /
плотность льда

 /
плотность алмаза

 /
плотность железа

 /
плотность меди

 /
плотность серебра

 /
плотность свинца

 /
плотность золота

 /
плотность платины

Использует

Относительная плотность также может помочь количественно оценить плавучесть вещества в жидкости или газе или определить плотность неизвестного вещества по известной плотности другого. Относительная плотность часто используется геологами и минералогами для определения содержания минералов в породе или другом образце. Геммологи используют его как вспомогательное средство при идентификации драгоценных камней . Вода предпочтительна в качестве эталона, потому что измерения затем легко проводить в полевых условиях (см. Ниже примеры методов измерения).

Поскольку основным применением измерений относительной плотности в промышленности является определение концентраций веществ в водных растворах, которые можно найти в таблицах зависимости RD от концентрации, чрезвычайно важно, чтобы аналитик вводил таблицу с правильной формой относительной плотности. Например, в пивоваренной промышленности таблица Плато , в которой указана концентрация сахарозы по массе в сравнении с истинным RD, изначально была (20 ° C / 4 ° C) и основана на измерениях плотности растворов сахарозы, полученных при лабораторной температуре (20 ° C / 4 ° C)

° C), но с учетом плотности воды при 4 ° C, что очень близко к температуре, при которой вода имеет максимальную плотность ρ ( H2O ) равным 0,999972 г / см 3 (или 62,43 фунт · фут -3 ). Таблица ASBC, используемая сегодня в Северной Америке, в то время как она получена из исходной таблицы Платона, предназначена для измерений кажущейся относительной плотности при (20 ° C / 20 ° C) по шкале IPTS-68, где плотность воды составляет 0,9982071 г / см 3 . В производстве сахара, безалкогольных напитков, меда, фруктовых соков и смежных отраслях массовая концентрация сахарозы взята из этой работы, в которой используется SG (17,5 ° C / 17,5 ° C). В качестве последнего примера британские единицы RD основаны на эталонной температуре и температуре образца 60 ° F и, следовательно, составляют (15,56 ° C / 15,56 ° C).

Плотность воды: аномалия

Аномалия заключается в том, что жидкое состояние увеличивает
плотность до температуры в 4°С, а далее — понижается. Другими словами, именно в
этом отрезке вода достигает максимальной плотности. Но в других агрегатных
состояниях параметр становится на порядок ниже: у пара его сложно рассчитать,
он практически невесомый, а лёд и снег меньше почти на 100 кг.

Аномалии плотности воды вызывают следующие явления:

• заморозка приводит к расширению, отсюда объем возрастает, но плотность снижается;
• плотность льда ниже, чем концентрация в жидком состоянии, несмотря на одинаковый источник — воду;
• вода имеет низкий коэффициент расширения и сжатия.

Отклонение в полной мере демонстрируется на примере льда. Он
не тонет, поскольку его плотность меньше, чем у воды. Аналогичная ситуация
складывается со снегом — он плавает на поверхности, пока не растает. При
смешивании талой воды с обычной на поверхности появляются видимые разводы — это
эффект смешивания, когда жидкость набирает аналогичную концентрацию. Однако в
похожей ситуации с топливом или маслами такое не пройдет, они останутся на поверхности.
Растаявший снег всё ещё вода, а другие жидкости ей не станут.

Свойство плотности имеет большое значение для живых
организмов. Из-за него водоемы промерзают сверху вниз, позволяя выжить
находящимся подо льдом формам жизни. Уникальные характеристики воды с её тремя
состояниями только подтверждают мысль, что природа полностью гармонична.

Как оценивается показатель

Вода, так же как все другие химические вещества, может находиться в различных агрегатных формах, количественные характеристики каждой из них имеют большое значение. Чаще всего возникает потребность в определении плотности воды в жидком состоянии. Проводить измерение можно с помощью следующих устройств и приспособлений:

• ареометр,
• специальный стеклянный сосуд – пикнометр.

Оба метода известны со времен зарождения научных исследований, правомерность использования и точность полученных значений как для пресной, так и для морской воды доказана многолетней общемировой практикой. Измерения позволяют оценить качество водной продукции, поступающей из центральных городских сетей, колодцев, скважин, выявить ее соответствие санитарным нормам. Плотность соленой воды морей – важная информация для экологов, океанологов, гидробиологов и кораблестроителей.

Быстрее и проще узнать значение плотности с помощью ареометра, который представляет собой поплавок с градуированной шкалой в верхней части. Его нужно поместить в жидкость, налитую в высокий стеклянный сосуд, например в мерный цилиндр, так, чтобы он свободно плавал, не прикасаясь к стенкам. Ареометр всплывет на некоторую высоту, после чего нужно записать значение шкалы, на уровне которого находится нижний край мениска.

Можно определить плотность воды, любой другой жидкости с помощью пикнометра. Так называется маленький сосуд со строго определенным объемом. Его нужно взвесить пустым, затем – с дистиллятом. На последнем этапе определить вес контрольной пробы. На основании трех полученных цифр проводят расчеты по формуле и получают конечный результат.

Что такое плотность воды?

Вода уникальна тем, что это единственная материя, встречающаяся
в трёх различных состояниях. Соответственно, в жидком она встречается
повсеместно — это можно назвать исходной формой. Её твердое состояние — лёд,
снег, а газообразное — водяной пар. Вещество в любой форме имеет одно
химическое обозначение — H 2 O.

Каждая форма состояния воды имеет собственную
характеристику:

• снег — мягкий, рыхлый, концентрация низкая;
• лёд — твердый, концентрация также ниже,
• вода — текучая: наиболее высокий показатель, достигаемый при 4°C;
• а водяные пары — не имеют формы, а плотность неизмерима.

Кроме того, твердая форма всегда имеет отрицательную температуру,
то есть всегда холодная. Вода, в свою очередь, бывает любой температуры, но при
высокой начинает испаряться — так, пар бывает только горячим. Впрочем, он
остывает при смешивании с воздухом и растворяется, поднимаясь выше от
источника.

Отличаются и другие характеристики: снег быстро растает,
если его поместить в воду, а лёд будет какое-то время плавать. Снежную массу и
воду можно окрашивать, а лёд и пар — нет. Конечно, получить цветные льдинки
возможно, но для этого нужно замораживать окрашенную воду. Однако, следует
учесть, что такое окрашивание может незначительно изменить параметр плотности из-за
использованного красителя.

Плотность воды по-своему уникальна, поскольку замерзшей она
имеет вес меньший, чем обычно. Соответственно, параметр также снижается. Иначе
говоря, замерзшая вода на разных стадиях заморозки будет иметь вес всё меньше и
меньше. Так, полностью заледеневшая вода имеет массу меньшую, чем снег. А
водяной пар весит и того меньше, следовательно, его плотность также уменьшается
и как её определить — неизвестно.

Параметр вычисляется массой, разделенной на единицы объема в
кг на м³. Другие особенности:

1. Вода может иметь разную массу и, следовательно, концентрацию из-за количества примесей и добавок.
2. Плотность чистой воды зависит от температуры: снижается как при росте, так и при снижении до минуса.
3. Не все жидкости — вода. Так, к примеру, плотность воды и бензина различна, несмотря на общую характеристику равномерного понижения при нагреве.

Максимальный зарегистрированный параметр составил 1000кг на
м³ при температуре в пределах 3-4°C. Увеличение и снижение показали схожие
результаты на понижение плотности. Можно сделать вывод, что наибольшую
плотность вода имеет в этом температурном диапазоне.

Закон Архимеда

Этот закон известен преимущественно не своей формулировкой, а историей его возникновения.

Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом, не причиняя вреда самой короне. То есть, нельзя ее расплавить или в чем-нибудь растворить.

Взвесить корону Архимеду труда не составило, но этого было мало — нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.

Это можно сделать по формуле плотности.

Формула плотности тела ρ = m/V ρ — плотность тела [кг/м^3] m — масса тела V — объем тела

Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.

Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (по легенде он даже не оделся).

Закон Архимеда

Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.

На поверхность твердого тела, погруженного в жидкость или газ, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.

Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой или силой Архимеда. Истинная причина появления выталкивающей силы — наличие различного гидростатического давления в разных точках жидкости.

Сила Архимеда FАрх = ρж * g * Vпогр ρ ж — плотность жидкости [кг/м^3] V погр — объем погруженной части тела g — ускорение свободного падения [м/с^2] На планете Земля: g = 9,8 м/с^2

А теперь давайте порешаем задачки.

Задача 1

В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? (Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой).

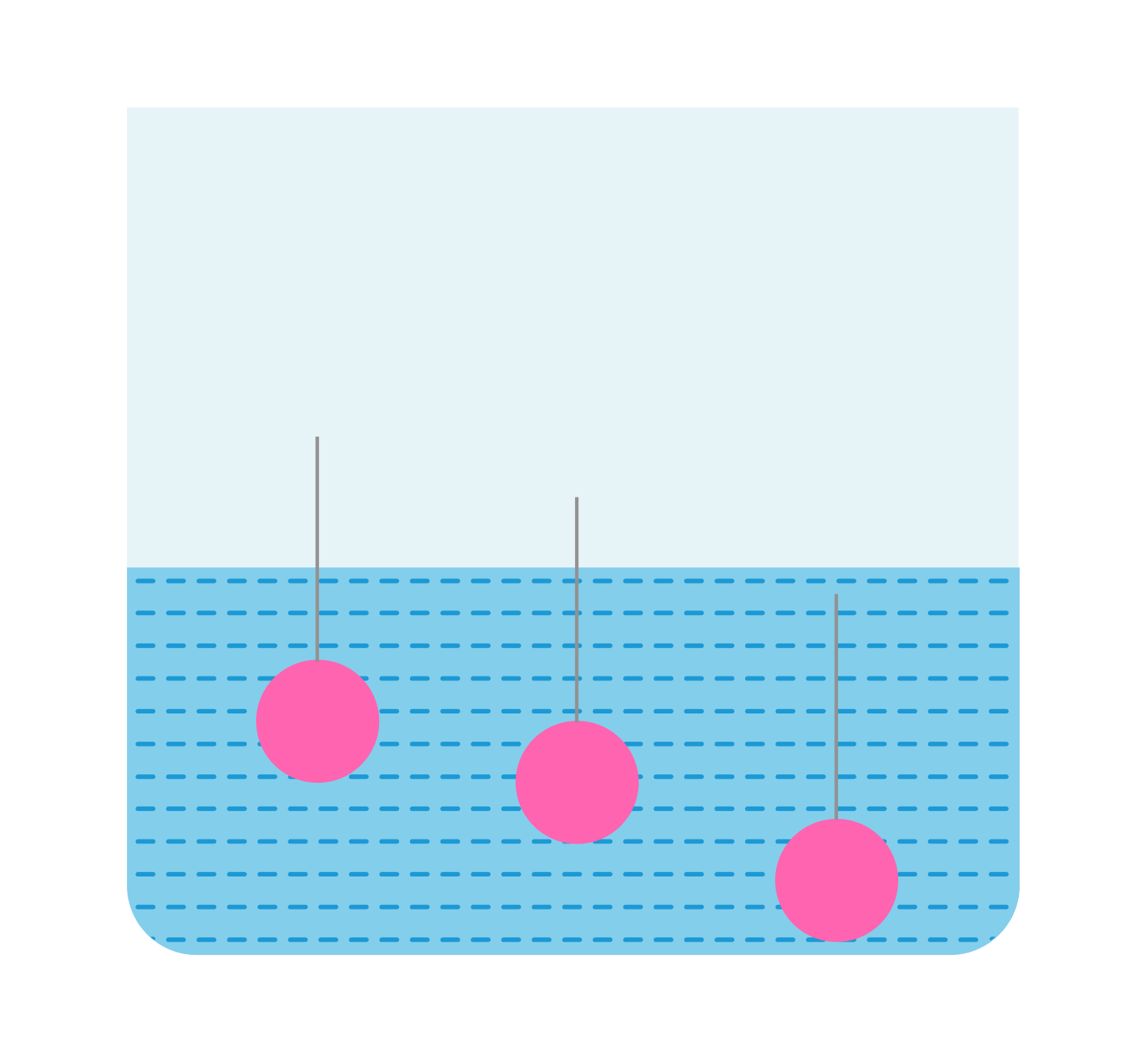
Решение:

Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.

Задача 2

На поверхности воды плавают бруски из дерева, пробки и льда. Укажите, какой брусок из пробки, а какой изо льда? Какая существует зависимость между плотностью тела и объемом этого тела над водой?

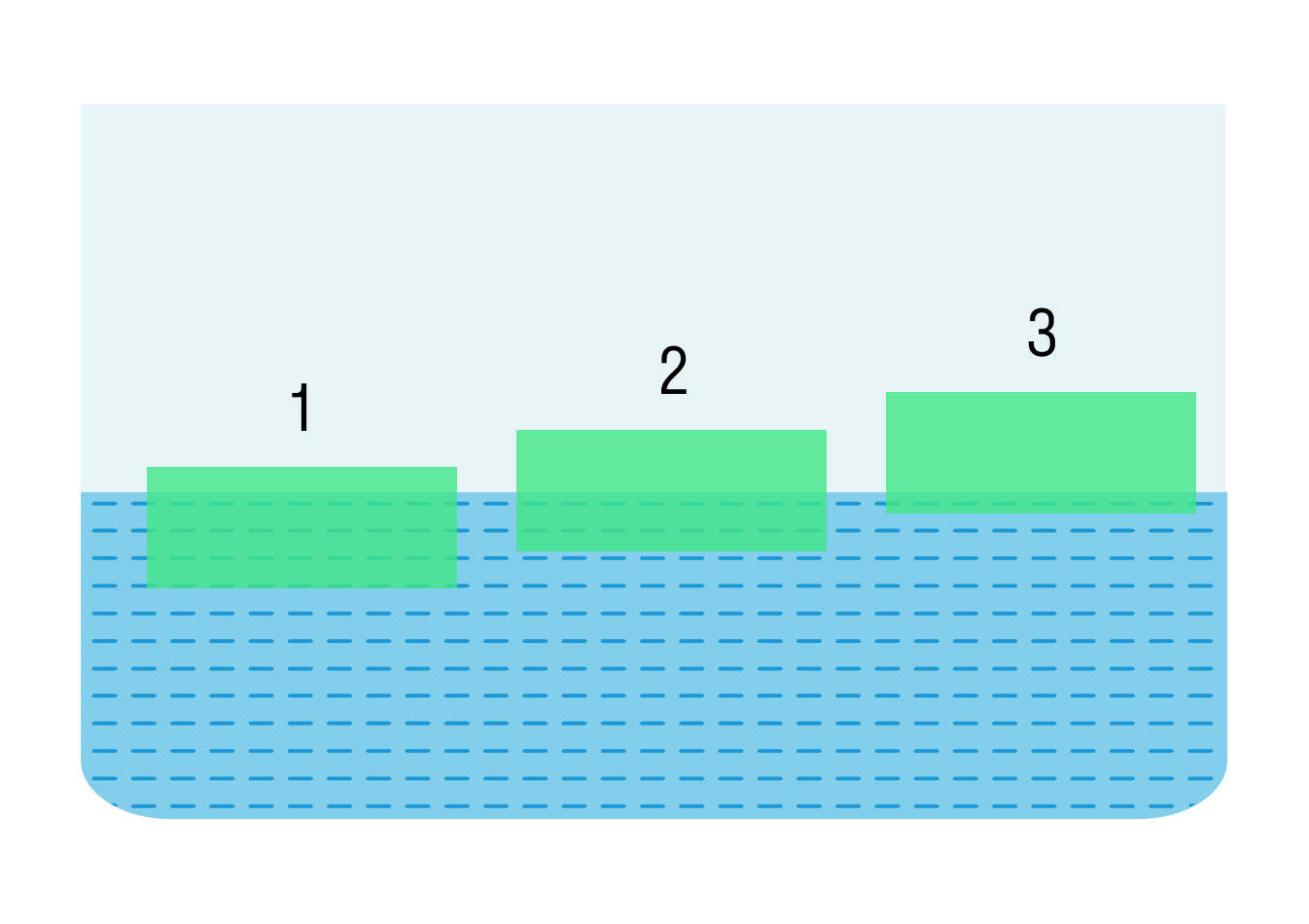
Решение:

Чем меньше плотность тела, тем большая часть его находится над водой. Дерево плотнее пробки, а лед плотнее дерева. Значит изо льда — материал №1, а из пробки — №3.

Задача 3

На графике показана зависимость модуля силы Архимеда FАрх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ускорение свободного падения принять равным 10 м/с2.

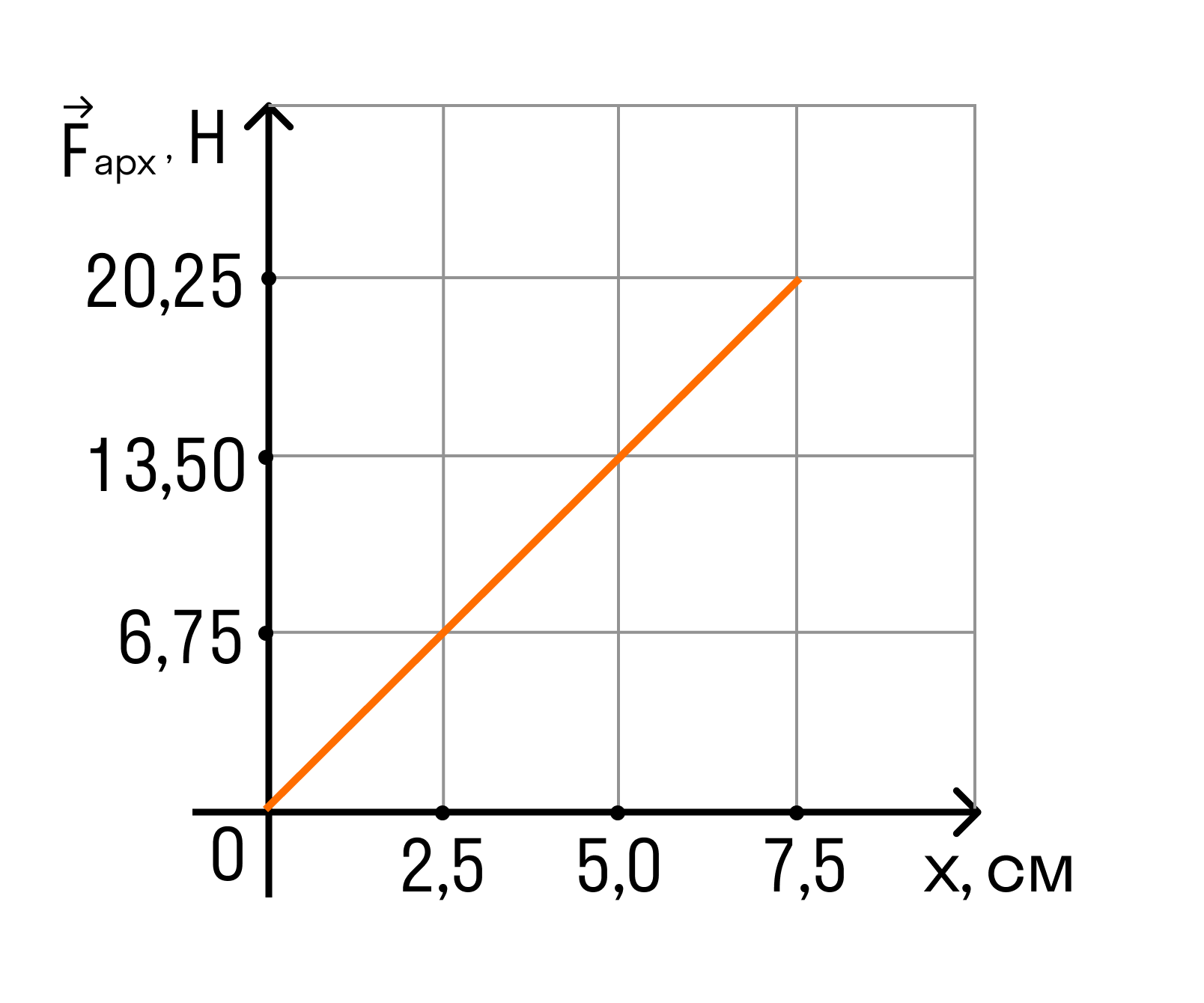
Решение:

Сила Архимеда, действующая на кубик равна F_Арх = ρ_ж * g * V_погр

V — объём погруженной части кубика,

ρ — плотность жидкости.

Учитывая, что нижнее основание кубика всё время параллельно поверхности жидкости, можем записать:

F_Арх = ρ_ж * g * V_{погр = ρж * g * a2 * x}

а — длина стороны кубика.

Выразим плотность:

ρ = F_Арх / (g * a2 * x)

Рассматривая любую точку данного графика, получим:

ρ = F_Арх / (g * a2 * x) = 20,25 / (10 * 7,5 * 10-2) = 2700 кг/м3

Ответ: плотность жидкости равна 2700 кг/м3

Задача 4

В сосуде с водой, не касаясь стенок и дна, плавает деревянный кубик с длиной ребра 20 см. Кубик вынимают из воды, заменяют половину его объёма на материал, плотность которого в 6 раз больше плотности древесины, и помещают получившийся составной кубик обратно в сосуд с водой. На сколько увеличится модуль силы Архимеда, действующей на кубик? (Плотность сосны — 400 кг/м3.)

Решение:

В первом случае кубик плавает в воде, а это значит, что сила тяжести уравновешивается силой Архимеда:

F_Арх1 = mg = ρ_т * g * a3 = 400 * 0,23 * 10 = 32 Н

После замены части кубика его средняя плотность станет равной

0,5 * 400 + 0,5 * 2400 = 1400 кг/м3

Получившаяся плотность больше плотности воды = 100 кг/м3. Это значит, что во втором случае кубик полностью погрузится в воду. Сила Архимеда в этом случае будет равна:

F_Арх2 = ρ_т * g * V_т = 1000 * 10 * 0,23 = 80 Н

Отсюда получаем, что сила Архимеда увеличится на 48 Н.

Ответ: сила Архимеда увеличится 48 Н