Повышенная сила

Содержание

• 1 Определение силы
• 2 Типы силы и их значение в тренировках 2.1 Сила: ее качества 2.1.1 Максимальная сила
• 2.1.2 Мощность
• 2.1.3 Мышечная выносливость

2.2 Сила: кривая силы — времени

• 2.2.1 Стартовая сила

2.2.2 Взрывная сила или темп развития силы
2.2.3 Мощность
2.2.4 Максимальная сила
2.3 Сила: мышечная деятельность

• 2.3.1 Концентрическая сила

2.3.2 Изометрическая сила
2.3.3 Эксцентрическая сила
2.4 Сила: отношение к массе тела

• 2.4.1 Абсолютная сила

2.4.2 Относительная сила
2.5 Сила: степень специфичности

• 2.5.1 Общая сила

2.5.2 Специфическая сила
2.5.3 Запас силы
3 Оценка максимальной, максимальной произвольной, абсолютной и относительной силы мышц

• 3.1 Тестирование

4

Абсолютная и относительная сила

Оценивая величину усилия в том или ином упражне­нии или простом движении, применяют термины «абсо­лютная» и «относительная» сила.

Абсолютная сила — предельное, максимальное усилие, которое спортсмен может развить в динамичес­ком или статическом режиме. Примером проявления абсолютной силы в динамическом режиме является под­нимание штанги или приседание со штангой предельного веса. В статическом режиме абсолютная сила может быть проявлена, например, когда максимальное усилие прилагается к неподвижному объекту («выжимание» неподвижно закрепленной штанги).

Относительная сила — величина силы, прихо­дящаяся на 1 кг веса спортсмена. Этот показатель при­меняется в основном для того, чтобы объективно срав­нить силовую подготовленность различных спортсменов.

Энергетические системы.

Что касается физических упражнений, область знаний спортивной физиологии включает изучение того, как организм вырабатывает энергию для мышечной работы. Энергия для сокращения мышц поступает в форме аденозинтрифосфата (АТФ), он получается в результате расщепления пищи из рациона.

Аденозинтрифосфат

Первоначально энергия в форме белков, жиров и углеводов преобразуется различными ферментативными путями, которые расщепляют пищу и в конечном итоге приводят к образованию АТФ. Для удовлетворения повышенных потребностей в АТФ при физических нагрузках в организме усиливаются химические реакции, обеспечивающие поставку АТФ.

Аэробный метаболизм не обеспечивает максимальной мощности мышц, при этом выполняемая работа в умеренной мощностной зоне (аэробная нагрузка) может поддерживаться в течение длительного времени. При таком типе метаболизма наше тело сначала использует свободный кислород, доступный в организме. Затем поддержка устойчивого состояния, при котором будет достигаться равновесное потребление и обеспечение организмом кислорода, будет зависеть от возможностей дыхательной и сердечно-сосудистой систем.

Сила упругости

Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.

Закон Гука

Сила упругости направлена противоположно деформации.

Так как тело представляем в виде материальной точки, силу можно изображать с центра

При последовательном соединении, например, пружин жесткость рассчитывается по формуле

При параллельном соединении жесткость

Жесткость образца. Модуль Юнга.

Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.

Подробнее о свойствах твердых тел здесь.

Быстрота как необходимая характеристика тем­па движений

Эта разновидность быстроты исключи­тельно важна в упражнениях циклического характера. Она представляет собой способность быстро чередовать «включения» и «выключения» необходимых мышечных групп, т. е. сокращение и расслабление их. Эта способ­ность позволяет не только увеличивать темп движений, но и выполнять каждое движение более эффективно, с меньшей затратой сил и энергии. Чем быстрее происхо­дит сокращение и расслабление мышцы, тем большее время она имеет для отдыха.

Не удивительно поэтому, что специальные скорост­ные упражнения, направленные на развитие темпа дви­жений, должны составлять основу скоростной трениров­ки спортсменов в видах спорта циклического характера. Каждое циклическое движение представляет собой со­четание возбуждения и торможения (работы и расслаб­ления) одной группы мышц с одновременным торможе­нием и возбуждением другой — мышц-антагонистов. При невысоком темпе это чередование происходит до­вольно четко и безошибочно. При повышении темпа движений, в силу того что процесс торможения развива­ется несколько медленнее, чем процесс возбуждения, наступает такой момент, когда возбуждение обеих групп мышц частично совпадает. Тогда возникает так называ­емая скоростная напряженность мышц, не позволяющая выдерживать подобный темп и тем более его увели­чивать. Скорость перехода мышцы от состояния возбуж­дения к состоянию торможения и обратно индивидуаль­на. Она может несколько повышаться под влиянием специальной тренировки, однако предпосылки к этому являются качеством врожденным, поэтому специальная тренировка у одного спортсмена дает больший эффект, а у другого — меньший.

В абсолютном большинстве видов спорта все эти разновидности скоростных качеств проявляются в соче­тании. Например, результат в спринтерском беге зависит и от реакции на старте, и от быстроты каждого одиноч­ного движения, и от развитого на дистанции темпа.

См.: Развитие способности к высокому темпу движений

См. также Физиологическая характеристика быстроты

Вайцеховский С. М. Книга тренера. — М.: Физкультура и спорт, 1971. 312 с. — Воспитание быстроты. – С. 186-188.

Возможности силы

Существуют различные способы измерения физической силы человека или населения. Анализ силовых возможностей обычно проводится в области эргономики, где конкретная задача (например, подъем груза, толкание тележки и т. Д.) И / или поза оценивается и сравнивается с возможностями той части населения, в которой выполняется задача. предназначен для. В таких случаях обычно используются внешние реактивные моменты и силы в соединениях. Силовые возможности сустава обозначаются количеством момента, который сила мышц может создать в суставе для противодействия внешнему моменту.

Скелетные мышцы создают в суставах реактивные силы и моменты. Чтобы избежать травм или утомления, когда человек выполняет какую-либо задачу, например толкает или поднимает груз, внешние моменты, создаваемые в суставах из-за нагрузки в руке и веса сегментов тела, должны быть в идеале меньше, чем мышечный момент. сильные стороны в суставе.

Одна из первых моделей в сагиттальной плоскости для прогнозирования силы была разработана Чаффином в 1969 году. На основе этой модели внешние моменты в каждом суставе не должны превышать моменты силы мышц в этом суставе.

M _{j / L} <S _j

Где S _j — момент силы мышц в суставе j, а M _{j / L} — внешний момент в суставе j, вызванный нагрузкой, L и сегментами тела, предшествующими суставу, в нисходящем анализе.

Анализ сверху вниз — это метод расчета реактивных моментов и сил в каждом суставе, начиная с руки, вплоть до голеностопного сустава и стопы. В 6-сегментной модели рассматриваются суставы локтя, плеча, диска L5 / S1 позвоночника , бедра, колена и лодыжки. При ручных расчетах обычно игнорируют лучезапястный сустав. Программное обеспечение, предназначенное для такого расчета, также использует лучезапястный сустав, разделяя нижнюю часть руки на сегменты кисти и предплечья.

Сила тяготения

В 1682 году Исаак Ньютон открыл Закон Всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон Всемирного тяготения F = GMm/R2 F — сила тяготения M — масса первого тела (часто планеты) m — масса второго тела R — расстояние между телами G — гравитационная постоянная G = 6.67 × 10-11 м3 кг-1 с-2

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.

Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.

Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.

Приливы и отливы существуют благодаря Закону Всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей

Несколько лет назад ученые открыли такое явление, как гравитационные волны — но это не тоже самое, что гравитация:

Сила в физике

Сила – мера взаимодействия тел. Взаимное действие тел друг на друга полностью описывает процессы, связанные с изменением скорости или деформацией тел.

Как физическая величина сила имеет единицу измерения (в системе СИ – Ньютон) и прибор для ее измерения – динамометр. Принцип действия силомера основан на сравнении силы, действующей на тело, с силой упругости пружины динамометра.

За силу в 1 ньютон принята сила, под действием которой тело массой 1 кг изменяет свою скорость на 1 м за 1 секунду.

Сила как векторная величина определяется:

• направлением действия;
• точкой приложения;
• модулем, абсолютной величиной.

Описывая взаимодействие, обязательно указывают эти параметры.

Виды природных взаимодействий: гравитационные, электромагнитные, сильные, слабые. Гравитационные силы (сила всемирного тяготения с ее разновидностью – силой тяжести) существуют благодаря влиянию гравитационных полей, окружающих любое тело, имеющее массу. Исследование полей гравитации не закончено до сих пор. Найти источник поля пока не представляется возможным.

Больший ряд сил возникает вследствие электромагнитного взаимодействия атомов, из которых состоит вещество.

Правило моментов

Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.

Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.

Это условие выполняется относительно любой точки.

Правило моментов M1 + M2 +…+ Mn = M’1 + M’2 +…+ M’n M1 + M2 +…+ Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке

Давайте рассмотрим этот закон на примере задач.

Задача 1

К левому концу невесомого стержня прикреплен груз массой 3 кг.

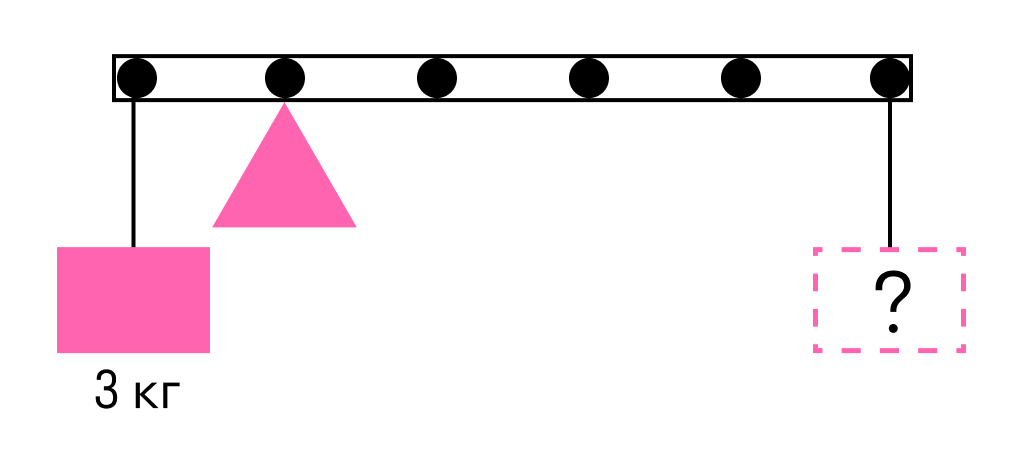
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

Решение:

Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.

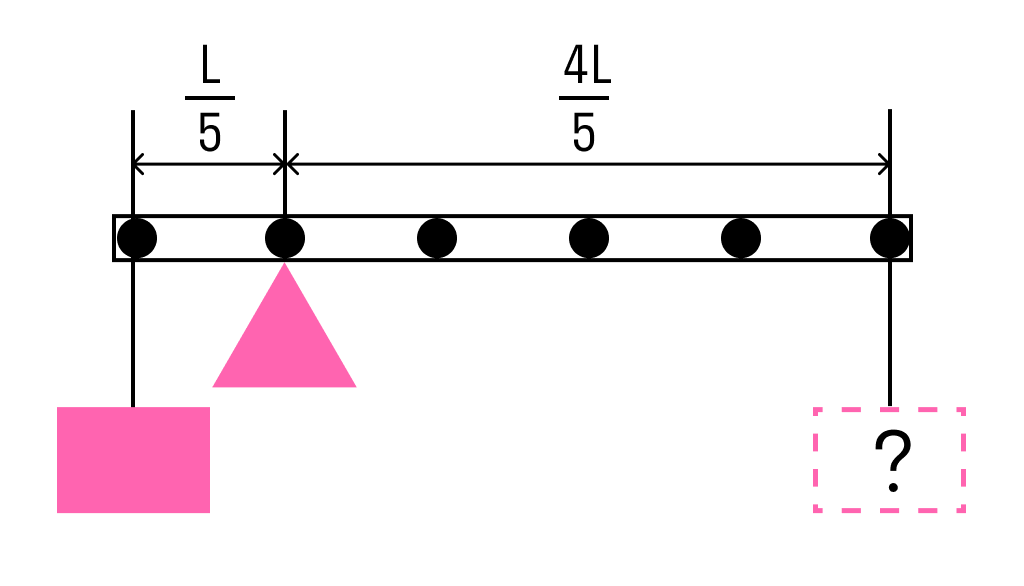
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг

Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг

Задача 2

Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

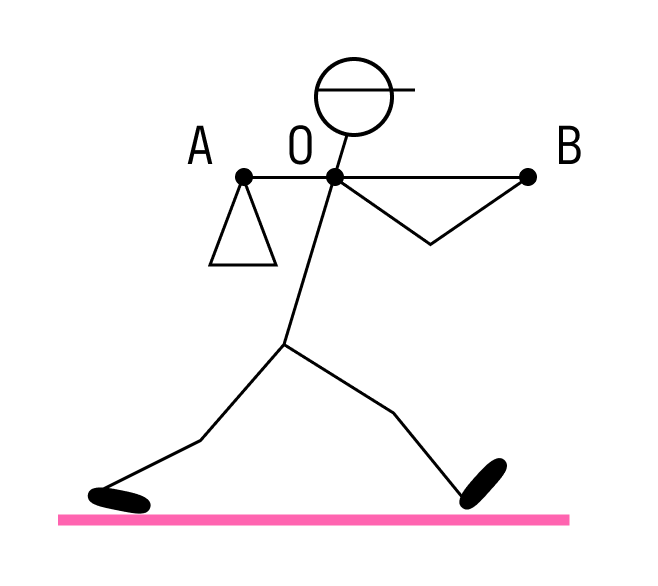
Решение:

По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:

|OA|=FB/FA)*|OB|=30/80*80=30 см

Ответ: расстояние ОА равно 30 см

Задача 3

Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

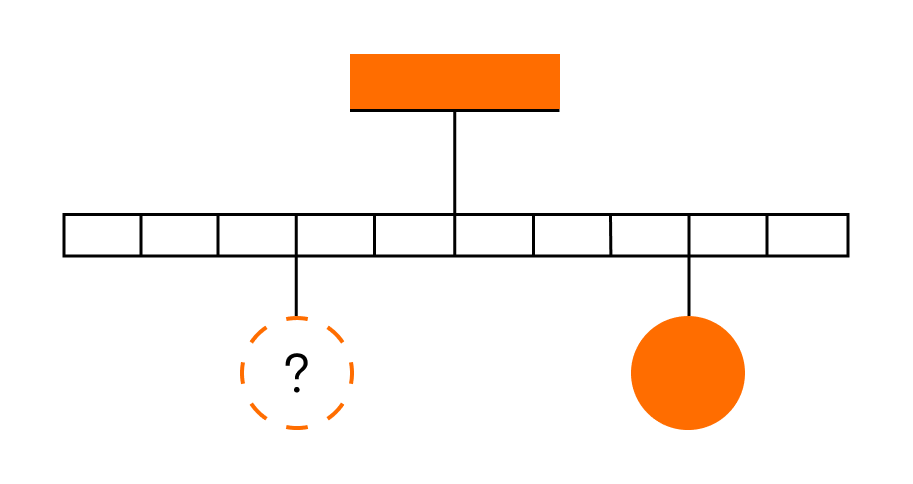
Решение:

По правилу рычага m1g*l1=m2g*l2

Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг

Ответ: Масса груза равна 0,3 кг

Задача 4

На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?

Решение:

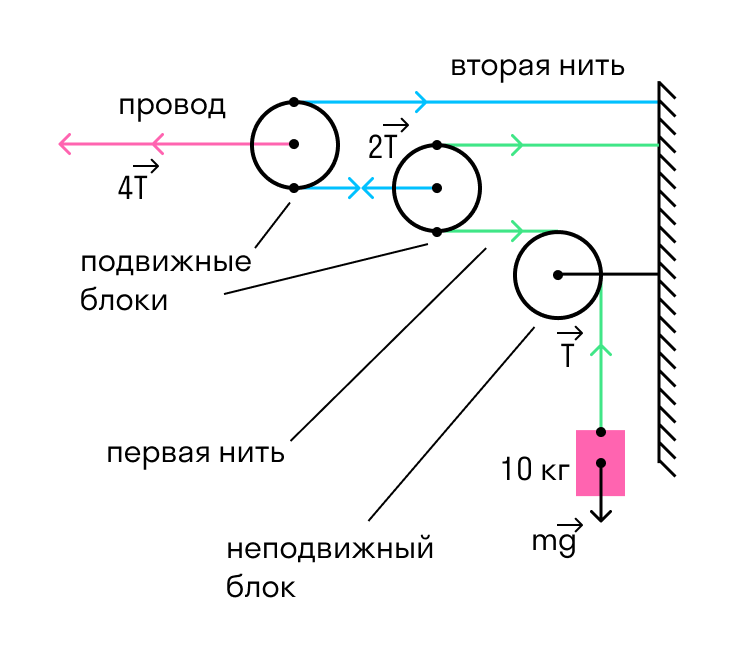
Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.

Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н

Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно

4T = 4*100= 400 Н

Ответ: натяжение провода равно 400 Н

Задача 5 — a.k.a самая сложная задачка

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?

Решение:

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести

mg=F*5/0,8=120*5/0,8=750Н

Ответ: модуль силы тяжести, действующей на груз равен 750 Н

Упражнения и нормативы по ОФП

Общеустановленных, единых нормативов по ОФП не существует. Каждая организация (школа, ВУЗ, ВС, правоохранительные органы) опираются на внутриведомственные документы. Тесты составляют из базовых упражнений.

Бег на длинную дистанцию – этот норматив существует для проверки выносливости.

Спринт или челночный бег – упражнения для оценки быстроты и ловкости.

Подтягивания на перекладине и отжимания – характеризуют силу мышц спины, рук и плечевого пояса.

Подъемы туловища из положения лёжа на спине – помогают оценить развитие мышц брюшного пресса.

Наклоны вперед – по глубине наклона определяют гибкость.

Учимся летать

В серии книг Дугласа Адамса «‎Автостопом по Галактике»‎ говорится, что летать — это просто промахиваться мимо Земли. Если ты промахнулся мимо Земли и достиг первой космической скорости 7,9 км/с, то ты стал искусственным спутником Земли.

Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него так получалось, аппарат должен иметь начальную скорость, равную или большую первой космической скорости.

Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы.

Подробнее о возможностях полетов и невесомости читайте в нашей статье про вес тела.

Второй закон Ньютона

Равнодействующая всех сил приложенных к телу (векторная сумма всех сил)
($\bar{F}$) равна производной от импульса тела по времени:

где $\bar{p}=m \bar{v}$ — импульс тела, m–масса рассматриваемого тела,
$\bar{v}$ — скорость. Надо отметить, что уравнение (1) строго применимо только относительно
материальной точки. Если рассматривается протяженное тело, то под скоростью понимают скорость движения центра масс тела.

Если масса материальной точки (m)не изменяется во времени, то формула, определяющая результирующую силу, приложенную к ней
(второй закон Ньютона) можно представить в виде:

где $\bar{a}$ – ускорение, которое материальная точка приобретает в результате
воздействия на нее силы. Выражение (2) показывает то, что если
$\bar{F}$=0, то тело (материальная точка) движется равномерно и прямолинейно или покоится.

Если сила, приложенная к телу, является постоянной (по модулю и направлению), то формулу для нее можно представить в виде:

Анаэробный гликолиз.

Глюкоза Накопленный в мышцах гликоген можно разделить на глюкозу, а затем использовать глюкозу для получения энергии. Гликолиз является первой частью этого процесса, который происходит без использования кислорода и, следовательно, считается анаэробным. Во время гликолиза каждая молекула глюкозы расщепляется на две молекулы пировиноградной кислоты, и энергия высвобождается с образованием четырех молекул АТФ для каждой молекулы глюкозы.

Молекулы пировиноградной кислоты могут использоваться митохондриями в мышечных клетках, реагируя с кислородом, и обеспечивать молекулы АТФ, но если упражнение слишком интенсивное, то, вероятно, кислорода недостаточно, поэтому пировиноградная кислота превращается в молочную кислоту.

Другой характеристикой системы гликоген-молочная кислота является то, что она может образовывать молекулы АТФ примерно в 2,5 раза быстрее, чем окислительный механизм митохондрий. Поэтому, когда большое количество АТФ требуется для коротких или умеренных сокращений мышц, механизм анаэробного гликолиза может быть использован в качестве быстрого источника энергии.

В оптимальных условиях система гликоген-молочная кислота может обеспечивать максимальную мышечную активность от 70 до 100 секунд в дополнение к 8-10 секундам, предоставляемым фосфагеновой системой, хотя и при несколько сниженной мышечной силе.

Понятие о силе

Вопрос, что такое сила в физике, начнем рассматривать с ее определения. Под ней полагают величину, способную изменять количество движения рассматриваемого тела. Математическое выражение для этого определения выглядит так:

Здесь dp¯ — это изменение количества движения (иначе его называют импульсом), dt — промежуток времени, за который оно изменяется. Отсюда видно, что F¯ (сила) является вектором, то есть для ее определения необходимо знать, как модуль (абсолютное значение), так и направление ее приложения.

Как известно, импульс измеряется в кг*м/с. Это означает, что F¯ вычисляется в кг*м/с2. Эта единица измерения получила название ньютона (Н) в СИ. Поскольку единица м/с2 — это мера измерения линейного ускорения в классической механике, то из определения силы автоматически следует 2-й закон Исаака Ньютона:

В такой формуле a¯ = dv¯/dt — ускорение.

Эта формула силы в физике показывает, что в ньютоновской механике величина F¯ характеризуется ускорением, которое она может сообщить телу с массой m.

Физическое качество БЫСТРОТА

Быстрота – это комплекс свойств, непосредственно определяющих скоростные характеристики движения, а также время двигательной реакции. Способность человека совершать двигательные действия в минимальный для данных условий отрезок времени.

В скалолазании данное физическое качество определяющую роль играет в дисциплине “скорость”.

Психологические характеристики быстроты

С точки зрения психологии быстрота — это способность управлять временными признаками движения, отражение в сознании спортсмена продолжительности, темпа и ритма движения.

Быстрота движений обусловливается, в первую очередь, соответствующей деятельностью коры головного мозга, подвижностью нервных процессов, вызывающих сокращение, напряжение и расслабление мышц, направляющих и координирующих действие спортсмена.

Залог быстроты находится в зависимости от трех основных компонентов:

1. Подвижность нервных процессов: только при очень быстрой смене возбуждения и торможения и соответствующей регуляции нервно-мышечного аппарата можно достигнуть высокой частоты движений с оптимальным приложением силы; продолжительность процесса восприятия, т. е. передача информации и начало ответного действия, составляет основу быстроты двигательной реакции.
2. Напряжение воли — достижение максимально возможной скорости в определенной степени зависит от сознательного акта применения усилия над собой.
3. Координационные центрально-нервные факторы в определенной мере влияют на частоту движений. Но не менее зависимой от них является быстрота отдельного движения. К координационным (центрально-нервным) факторам относится совокупность центрально-нервных координационных механизмов управления мышечным аппаратом и механизмов внутримышечной и межмышечной координации.С помощью координационных факторов, в частности, регулируются сократительные усилия мышц (группы мышц), соответствующие пику скорости движения (действия).

Формы проявления быстроты

Показатель, характеризующий быстроту как качество, определяется:

1. временем двигательной реакции (минимальное время, необходимое для начала действия в ответ на определенный раздражитель). Это время, затраченное спортсменом на начало действия в ответ на известное ему определенное раздражение, например звуковой сигнал старта (выстрел из стартового пистолета, свисток судьи). В данном случае латентным временем двигательной реакции будет время, затраченное спортсменом на восприятие звукового сигнала, обработку полученной информации, передачу импульса к действию как ответной реакции на раздражитель. Окончанием этого процесса считается момент, с которого начата двигательная активность спортсмена.
2. скоростью отдельного движения характеризуется психической организацией одиночного действия.
3. темпом (частотой одинаковых движений в единицу времени).

Если ходьба человека состоит из множества повторяющихся движений (шагов), то один шаг — отдельное движение. Скорость одного шага — это скорость отдельного движения. Скорость шагов — соответственно частота движений.

Эти три формы проявления быстроты не зависят друг от друга. Каждая из них имеет свои особенности, которые существуют во временных параметрах.

Средства и методы развития быстроты движений

Методы развития быстроты:

– метод многократного повторения скоростных упражнений с предельной и околопредельной интенсивностью, (в серии выполняется 3-6 по-»трений, за одно занятие выполняются 2 серии. Если в повторных попытках скорость снижается, то работа над развитием быстроты заканчивается, т.к. при этом начинает развиваться выносливость, а не быстрота);

– игровой метод (дает возможность комплексного развития скоростных качеств, поскольку имеет место воздействие на скорость двигательной реакции, на быстроту движений и другие действия, связанные с оперативным мышлением. Присущий играм высокий эмоциональный фон и коллективные взаимодействия способствуют проявлению скоростных возможностей).

Средствами для развития быстроты могут быть легкая атлетика, спортивные игры и др.

Силы вокруг нас (силы тяжести, трения, упругости)

1. Сила – термин, являющийся: а) кратким обозначением действия одного тела на другое; б) названием физической величины, характеризующей действие тел друг на друга (взаимодействие тел).

2. Признаки действия силы: меняется скорость и/или направление движения тела, меняются размеры и/или форма тела.

3. Динамометр – прибор для измерения сил. Единица силы в СИ – 1 Н (один ньютон).

4. На чертежах силу изображают в виде прямой стрелки, называемой вектором силы. Длина вектора символизирует числовое значение силы, а направление вектора указывает направление силы.

5. Если две силы: а) приложены к одному и тому же телу, б) направлены противоположно по одной прямой и в) имеют одинаковую величину, их называют уравновешенными силами.

6. Если на тело действуют только уравновешенные силы, то оно либо покоится, либо движется прямолинейно и равномерно. И наоборот.

7. Силой упругости называют силу, которая возникает при изменении формы и/или размеров тела. Вектор силы упругости всегда противонаправлен вектору той силы, которая вызвала деформацию. Сила упругости обусловлена взаимодействием частиц, из которых состоит тело.

• Силу, действующую на тело со стороны опоры, называют силой нормальной реакции.
• Закон Гука для силы упругости: F_упр = kx, где F_упр — модуль силы упругости, х — удлинение пружины.
• Прибор для измерения силы называют динамометром.
• Равнодействующей двух или нескольких сил называют силу, которая производит на тело такое же действие, как одновременное действие этих сил.

8. Силой трения называют силу, которая возникает при движении (или попытке вызвать движение) одного тела по поверхности другого. Она всегда направлена противоположно направлению скольжения (или направлению возможного скольжения) рассматриваемого тела.

• Основная причина возникновения сил трения скольжения и покоя — зацепление неровностей на поверхностях соприкасающихся тел.
• Модуль силы трения скольжения F_тр= μN, где N — модуль силы нормальной реакции, μ — коэффициент трения.
• Сила трения покоя возникает, когда пытаются сдвинуть одно из соприкасающихся тел относительно другого. Эта сила препятствует движению тел друг относительно друга.
• Сила трения покоя не превышает некоторой предельной величины, которую называют максимальной силой трения покоя. Обычно принимается, что максимальная сила трения покоя равна силе трения скольжения.
• Сила трения качения обычно намного меньше силы трения скольжения — на этом основано использование колеса.

9. Силой тяжести называют силу, с которой тело притягивается к планете. Сила тяжести всегда направлена к центру масс этой планеты. Модуль силы тяжести F_т = gm, где m — масса тела, g = 9,8 Н/кг. Точку приложения силы тяжести называют центром тяжести тела.

10. Весом тела называют силу, с которой это тело действует на свою опору или подвес. Условие равенства веса силе тяжести: тело и его опора (или подвес) должны покоиться или двигаться вместе прямолинейно и равномерно, при этом не должна действовать архимедова сила.

• Вес тела приложен к опоре или подвесу, а сила тяжести — к самому телу.
• Состояние, при котором вес тела равен нулю, называют состоянием невесомости. В состоянии невесомости находятся тела, на которые действует только сила тяжести.

11. Механизмы – устройства для преобразования движения и сил. Простые механизмы – наклонная плоскость (и ее разновидности: клин и винт) и рычаг (и его разновидности: ворот и блоки).

Схемы «Силы вокруг нас (силы тяжести, трения, упругости)».

Конспект по теме «Силы вокруг нас (силы тяжести, трения, упругости)».

Следующая тема: «Задачи на силы тяжести и вес тела»

Принципы силовой специфичности

Для достижения каждой конкретной цели необходимо придерживаться определенной силовой стратегии. В то время как движение очень тяжелого веса в медленном темпе будет развивать один вид силы, движение легкого веса в скоростной манере будет производить совсем другой ее вид. Например, для тренировки максимальной силы необходимо работать в очень низком диапазоне повторений с очень тяжелым весом, а для развития взрывной силы нужно поднимать умеренный вес в максимально быстром темпе.

Ниже мы представим 7 разновидностей силы, а вы определите, которая из них подойдет для вашей цели в данный период времени.

Рычаг

В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.

Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.

Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Правила выполнения упражнений

Правила выполнения силовых упражнений в целом соответствуют общим правилам выполнения любых физических упражнений, и основываются на принципах физического воспитания.

Силовые упражнения целесообразно выполнять при отсут­ствии утомления, при котором возбудимость ЦНС снижена.

Подбор силовых упражнений дол­жен осуществляться с учётом пола, возраста, уровня ОФП, развития психомоторики, мышечной силы, индивидуальности личности, с применением принципа доступности. При использовании средств атлетической гимнастики не­обходимо учитывать тип телосложения, основываясь на ант­ропометрических измерениях.

По сравнению с упражнениями другой направленности си­ловые упражнения оказывают большее воздействие на орга­низм. Очень серьёзно следует относиться к дыханию, особенно при выполнении упражнений, требующих максимальных уси­лий. Вдох должен совпадать с движением тела, при котором грудная клетка расширяется: при движении рук вверх, в сто­роны, при выпрямлении туловища. Сгибание туловища, опу­скание рук, сужение грудной клетки наиболее удобны для вы­доха.

Занятия атлетической гимнастикой обязательно должны дополняться утренней гимнастикой продолжительностью 30-60 мин, включающей в основном упражнения циклического характера, упражнения на гибкость, растяжку с чередовани­ем напряжения и расслабления.

Тренировка разных групп мышц

В целях гармоничного развития форм и массы тела, рельефа мышц, а также совершенствования координационных способ­ностей управления мышечным сокращением при выполнении силовых упражнений необходимо охватывать по возможности все основные группы мышц

Первостепенное внимание следует уделять развитию мышечных групп, которые имеют наиболь­шее значение в трудовых и жизненных ситуациях. К ним от­носятся сгибатели и разгибатели позвоночного столба, мышцы тазобедренных суставов, разгибатели рук и ног, большая груд­ная мышца, мышцы поясничной области и живота

Хорошо развитые мышцы живота способствуют нормальному функцио­нированию внутренних органов (вегетативных функций). При выполнении силовых упражнений следует помнить, что пояс­ничная область тела наиболее подвержена травмам в связи с перегрузками, возникающими при поднимании грузов.

Ошибки

Недопустимы частые натуживания. В большинстве случаев они сигнализируют о том, что нагрузка для организма велика и её необходимо снизить. Большие напряжения выполняются на полувдохе, в паузе между повторениями надо сделать один-два дыхательных цикла (вдох-выдох).

Следует помнить, что при выполнении силовых упражнений нельзя допускать задержки дыхания, когда без этого можно обойтись.

Юношам и девушкам 16-17 лет нежелательно упражнять­ся с предельными и околопредельными напряжениями.

Фосфокреатин – креатиновая система.

Креатин Фосфокреатин – химическое соединение, имеющее высокоэнергетическую фосфатную связь, которая может быть гидролизована, чтобы обеспечить энергию и повторно синтезировать АТФ. Это происходит в течение очень короткого времени. Следовательно, вся энергия, запасенная в мускулах, почти мгновенно доступна для сокращения мышц, так же как и энергия, запасенная в АТФ.

Хочешь помочь проекту? Отключи AdBlock, тем самым мы сможем получить доход за показ рекламы.

При выполнении коротких и быстрых движений, будь то спринт или рывок штанги, АТФ расщепляется на АДФ , в результате чего происходит ресинтез АТФ с помощью креатинфосфата. Этот метод является самым быстрым и простым способом получения энергии для сокращения мышц. Такой источник энергии может обеспечивать мышечное сокращение около 5 секунд, так как мышечные клетки хранят небольшое количество АТФ и креатинфосфата. Данная энергетическая система работает без кислорода и соответственно называется анаэробным методом производства энергии.

Таким образом, энергия из системы АТФ-фосфокреатин (хранящийся в мышцах) используется для максимально коротких всплесков мышечной силы.

Примеры решения задач

Пример

Задание. Уравнения $x=\alpha t^{3}, y=\beta t$ ($\alpha$ и
$\beta$ – постоянные коэффициенты) задают движение материальной точки массы m=const.
Как изменяется по модулю сила, которая действует на точку?

Решение. В качестве основы для решения задачи используем второй закон Ньютона в виде:

$\bar{F} = m\bar{a} (1.1)$

Зная законы изменения координат точки в зависимости от времени определим уравнения изменения составляющих ускорения.
Для этого найдем производные по времени от соответствующих координат:

$$
\begin{array}{c}
a_{x}=\frac{d^{2} x}{d t^{2}}=6 \alpha t(1.2) \\
a_{y}=\frac{d^{2} y}{d t^{2}}=0(1.3)
\end{array}
$$

Так как модуль ускорения равен:

$$a=\sqrt{a_{x}^{2}+a_{y}^{2}}(1.4)$$

то, учитывая выражения (1.2) и (1.3), получаем:

$a = 6 \alpha t (1.5)$

Так как a_y=0, то получаем, что сила, которая действует на нашу точку, направлена по оси X, так как направление ускорение
и силы совпадают, а мы получили:

$$\bar{a}=6 \alpha t \cdot \bar{i}(1.6)$$

где $\bar{i}$ – единичный вектор, направленный по оси X.

Исходя из второго закона Ньютона, имеем:

$$F=m \cdot 6 \alpha t, \bar{F}=m 6 \alpha t \cdot \bar{i}$$

Ответ. Так как $F=m \cdot 6 \alpha t$, то с течением времени сила увеличивается по модулю.

Слишком сложно?

Формула силы не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Два параллелепипеда лежат на горизонтальной поверхности. Они соприкасаются. Данные тела могут
скользить по поверхности опоры без трения. Масса одного тела равна m₁, второго — m₂. Первое тело толкнули с силой F.
Какова сила давления тел друг на друга (F)?

Решение. Сделаем рисунок.

Рассмотрим, какие силы приложены к первому телув момент толчка, запишем для него второй закон Ньютона:

$$\bar{F}_{0}+\bar{F}+m_{1} \bar{g}+\bar{N}=m_{1} \bar{a}(2.1)$$

где $m_{1} \bar{g}$ – сила тяжести,
$\bar{N}$ – реакция опоры,
$\bar{a}$ – ускорение тела.

В проекции на ось Xуравнение (2.1) примет вид:

$$F_{0}-F=m_{1} a \rightarrow F=F_{0}-m_{1} a(2.2)$$

Рассмотрим силы, приложенные к двум параллелепипедам как системе:

$$\bar{F}_{0}+\left(m_{1}+m_{2}\right) \bar{g}+\overline{N^{\prime}}=\left(m_{1}+m_{2}\right) \bar{a}(2.3)$$

В проекции на ось X уравнение (2.3) примет вид:

$$F_{0}=\left(m_{1}+m_{2}\right) a(2.4)$$

Из уравнения (2.4) выразим ускорение:

$$a=\frac{F_{0}}{m_{1}+m_{2}}$$

Подставим правую часть выражения (2.5) в (2.2) вместо ускорения:

$$F=F_{0}-m_{1} \cdot \frac{F_{0}}{m_{1}+m_{2}}$$

Ответ. $F=F_{0}-m_{1} \cdot \frac{F_{0}}{m_{1}+m_{2}}$

Читать дальше: Формула сопротивления.